十大常见的内部排序算法

所谓内部 (Internal) 排序，是指在计算机的主存而非外存中进行的排序。
所谓稳定 (Stable) 的排序算法，是指排序完后大小相等的元素的相对位置能保持不变。在以某一键值进行排序时（如基数排序），稳定性是十分重要的。
所谓原地排序算法 (In-place Sorting Algorithm)，是指除了函数调用所需的栈和固定数目的实例变量之外无序额外内存的排序算法。^[1]

Part 1 排序算法介绍

在这里，我们以从小到大排序为例介绍这些算法，所有的排序都在数组中进行：

1. 选择排序

选择排序 (Selection Sort) 思路是每次选择最小的元素交换到已经排好的部分的末尾。实现起来较为简易。

template <typename T>
void selection_sort(T* start, unsigned int scale) {
    for (int i = 0; i < scale - 1; ++i) {
        int min_index = i;
        for (int j = i + 1; j < scale; ++j) {
            if (start[j] < start[min_index]) {
                min_index = j;
            }
        }
        T exchange = start[i];
        start[i] = start[min_index];
        start[min_index] = exchange;
    }
}

选择排序是不稳定的排序算法：1 2 7 7 3 -> 1 2 3 7 7
选择排序的时间复杂度在一般情况下为 O(n²)，不存在更好或更差的情况。
空间复杂度为 O(1)，是原地排序算法。

2. 插入排序

插入排序 (Insertion Sort) 思路类似按高矮排队时新来了一个人的情况，这个人站到队尾后便开始与前面比他高的人不停地交换位置。元素越有序，对插入排序就越有利。

template <typename T>
void insertion_sort(T* start, const unsigned int scale) {
    for (int i = 1; i < scale; ++i) {
        for (int j = i; j > 0 && start[j] < start[j - 1]; --j) {
            T temp = start[j];
            start[j] = start[j - 1];
            start[j - 1] = temp;
        }
    }
} 

交换元素时不会改变相同元素的相对顺序，故插入排序是稳定的排序算法。
插入排序平均时间复杂度为 O(n²)，最好情况下（元素全部有序）时间复杂度为 O(n)，这是内层循环条件不满足；最坏情况是完全逆序时，这时需要把每次遍历到的元素交换到最开头。
空间复杂度为 O(1)，是原地排序。

3. 冒泡排序及其改进

冒泡排序 (Bubble Sort) 的思路是每次将未排序元素中最小或最大的交换到一端，形似因密度不同而不断冒出的气泡。由于每次都挑出最值，因此每挑出一次，下一次的最值就是上次的次最值，排在上次挑出值的后面。要注意挑出的最值位于遍历方向的末尾。

template <typename T>
void original_bubble_sort(T *data, int len) {
    for (int i = 0; i < len - 1; ++i) {
        for (int j = 1; j < len - i; ++j) {
            if (data[j] > data[j - 1]) {
                std::swap(data[j], data[j - 1]);
            }
        }
    }
}

冒泡排序是稳定的排序算法，由于交换的是相邻的元素，不会有相等的元素越过对方。
冒泡排序时间复杂度为 O(n²)，空间复杂度为 O(1)，属于原地排序。

但这还没完，冒泡排序显然还有优化的空间：

1. 有序时停止

在已经有序（即一轮比较后不发生任何交换）的情况下，可以停止排序了：

template <typename T>
void timelystop_bubble_sort(T *data, int len) {
    for (int i = 0; i < len - 1; ++i) {
        bool has_exchange = false;
        for (int j = 1; j < len - i; ++j) {
            if (data[j] > data[j - 1]) {
                std::swap(data[j], data[j - 1]);
                has_exchange = true;
            }
        }
        if (!has_exchange) break;
    }
}

此时，最好情况下（已有序）时间复杂度为 O(n)。

2. 确定有序边界

从全部有序的情况出发，进一步地，如果数组只是末尾有序，虽然不能直接退出排序，但可以省掉末尾的部分（开头有序没法省去，因为要从里面挑元素往后移动，即使开头的元素有序了，那也不是它们最终的位置）：

template <typename T>
void skipsorted_bubble_sort(T *data, int len) {
    int border = len;
    for (int i = 0; i < len - 1; ++i) {
        int last_exchange = 0;
        for (int j = 1; j < border; ++j) {
            if (data[j] < data[j - 1]) {
                std::swap(data[j], data[j - 1]);
                last_exchange = j;
            }
        }
        if (last_exchange == 0) break;
        border = last_exchange;
    }
}

此时最好的时间复杂度为 O(n)。

3. 鸡尾酒排序

鸡尾酒排序 (Cocktail Sort) 是“来回”的冒泡排序。传统的冒泡排序在升序时，最小元素在数组末尾会一点一点往上冒，而最大元素在起始却一趟就冒过去了。为了更好地平衡，可以在顺序冒一趟后倒序再来。这里我们直接在上面确定有序边界版本的冒泡排序上作修改：

template <typename T>
void skipsorted_cocktail_sort(T *data, int len) {
    int last_exchange = 0, first_exchange = len;
    int max_border = len, min_border = 0; // 两个都取不到
    for (int i = 0; i < len - 1; ++i) {
        for (int j = min_border + 1; j < max_border; ++j) {
            if (data[j] < data[j - 1]) {
                std::swap(data[j], data[j - 1]);
                last_exchange = j;
            }
        }
        if (last_exchange == 0) break;
        for (int j = last_exchange - 1; j > min_border; --j) {
            if (data[j] < data[j - 1]) {
                std::swap(data[j], data[j - 1]);
                first_exchange = j - 1;
            }
        }
        if (first_exchange == len) break;
        max_border = last_exchange;
        min_border = first_exchange;
    }
}

4. 希尔排序

希尔排序 (Shell Sort，以发明者的名字命名) 又称递减增量排序 (Diminishing Increment Sort)，它使用插入排序先使数组中任意间隔 h 的元素有序，然后按照一定的序列减小 h （要求 h 最后要以 1 结尾）并按减小的 h 排序。这里，我们使用 1/2(3^k-1) 作为希尔排序的递增序列，递增到小于数组长度的最大值，然后每次除以 3，直到等于 1：

template <typename T>
void shell_sort(T* start, int scale) {
    int span = 1;
    while (span < scale / 3) span = 3 * span + 1;
    while (span >= 1) {
        for (int i = span; i < scale; i++) {
            for (int j = i; j >= span && start[j] < start[j - span]; j-= span) {
                T temp = start[j];
                start[j] = start[j - span];
                start[j - span] = temp;
            }
        }
        span = span / 3;
    }
} 

希尔排序交换元素时会跨越一部分元素，因此可能改变相等元素的相对位置，是不稳定的排序算法：3 3 1 -> 1 3 3
希尔排序的时间复杂度似乎是无法准确描述的。这里给出的算法在最坏情况下的时间复杂度为 O(1.5)，空间复杂度为 O(1)，是原地排序。

5. 归并排序及其改进

归并排序 (Merge Sort) 是通过将已经排序好的两个小的子数组合并成大的数组实现的，传统上，归并排序需要一个辅助数组，在排序通过双指针时判断是把哪个小数组中的元素加入。这里我们用自顶向下的方法，先分割，直到无法再分割，然后通过函数栈的顺序调用来合并。

template <typename T>
class MergeSorts {
private:
    static T* auxiliary;
    static void merge(T* start, int low, int mid, int high) {
        int left_cursor = low,
            right_cursor = mid + 1;  // 指向第一个没加入的元素
        if (start[mid] <= start[mid + 1]) return; // 如果已经满足有序，直接返回
        for (int i = low; i <= high; ++i) {
            auxiliary[i] = start[i];
        }
        for (int i = low; i <= high; ++i) {  // 设计好循环的次数，保证不越界
            if (left_cursor > mid)
                start[i] = auxiliary[right_cursor++];  // 左边全加进去了加右边
            else if (right_cursor > high)
                start[i] = auxiliary[left_cursor++];  // 右边全加进去了加左边
            else if (auxiliary[left_cursor] > auxiliary[right_cursor])
                start[i] = auxiliary[right_cursor++]; // 否则就比左右大小决定
            else
                start[i] = auxiliary[left_cursor++];  // 注意排序稳定性（元素相等时）
        }
    }
    // 注意 low 和 high 能不能取到：这里都能取到
    // 如果 low 和 high 相等，直接返回，保证 merge 函数 low 和 high 差至少为 2；
    // 差 1 的时候 mid 与 low 相等，mid + 1 与
    // high 相等，不重叠
    static void merge_sort_TD(T* start, int low, int high) {
        if (high <= low)
            return;                        // Only one in selection.
        int mid = low + (high - low) / 2;  // Ensure mid <= high
        merge_sort_TD(start, low, mid);
        merge_sort_TD(start, mid + 1, high);
        merge(start, low, mid, high);
    }
public:
    static void merge_sort_TopDown(T* start, int scale) {
        auxiliary = new T[scale];
        merge_sort_TD(start, 0, scale - 1);
        delete[] auxiliary;
    }
};
template <typename T> T* MergeSorts<T>::auxiliary;

类似地，还有自底向上的归并排序，从最小单元开始逐步增大小数组的长度来合并：

static void merge_sort_UpBottom(T* start, int scale) {
    auxiliary = new T[scale];
    for (int sub_length = 1; sub_length < scale; sub_length *= 2) {
        for (int left_cursor = 0; left_cursor < scale - sub_length; left_cursor+= 2 * sub_length) {
            merge(start, left_cursor, left_cursor + sub_length - 1, std::mi(left_cursor + 2 * sub_length - 1, (scale - 1)));
        }
    }
    delete[] auxiliary;
}

这样看，归并排序是稳定的排序算法，归并时子数组的相对位置不改变，相等的元素也可以按照先后顺序并入最后的答案中。
如果采用树形结构描述归并排序的递归流程，由于每“层”中各次操作加起来（例如调用前 1/4，上 1/4，下 1/4，末 1/4）都得比较整个数组一遍，而有大约 log₂n 层（递归深度），故一般的时间复杂度为 O(nlogn)。考虑到针对有序子数组的优化，最好的情况下比较是 O(n) 的。
需要额外数组，空间复杂度为 O(n)。
但归并排序也有优化空间，可以通过在每层遍历时交换输入原数据的数组和辅助数组来减少归并时的数组复制：

// std::swap 会交换指针指向的对象，需要自己的交换函数
template <typename T> void swap_ptr(T *& a, T *& b) {
    T *temp = a;
    a = b;
    b = temp;
}
template <typename T>
void merge(T* start, T* auxiliary, int low, int mid, int high) {
    int left_cursor = low,
        right_cursor = mid + 1;  // 指向第一个没加入的元素
    //if (start[mid] <= start[mid + 1])
    //    return;  //  不能使用这样的优化，因为在 auxiliary 和 start 交换优化时这两个数组根本不相等，没法把 auxiliary 写回
    for (int i = low; i <= high; ++i) {  // 设计好循环的次数，保证不越界
        if (left_cursor > mid)
            start[i] = auxiliary[right_cursor++];  // 左边全加进去了加右边
        else if (right_cursor > high)
            start[i] = auxiliary[left_cursor++];  // 右边全加进去了加左边
        else if (auxiliary[left_cursor] > auxiliary[right_cursor])
            start[i] = auxiliary[right_cursor++];
        else
            start[i] = auxiliary[left_cursor++];  // 否则就比左右大小决定
    }
}
template <typename T>
void merge_sort_TD(T* start, T* auxiliary, int low, int high) {
    if (high <= low)
        return;                        // Only one in selection.
    int mid = low + (high - low) / 2;  // Ensure mid <= high
    merge_sort_TD(auxiliary, start, low, mid);
    merge_sort_TD(auxiliary, start, mid + 1, high);
    merge(start, auxiliary, low, mid, high);
}
template <typename T>
void merge_sort_TopDown(T* start, int scale) {
    T *auxiliary = new T[scale];
    for (int i = 0; i < scale; ++i) {
        auxiliary[i] = start[i];
    }
    merge_sort_TD(start, auxiliary, 0, scale - 1);
    delete[] auxiliary;
}

6. 快速排序

快速排序 (Quick Sort) 被誉为是“20世纪对科学和工程领域的发展产生最大影响力的十大算法”^[2]，在快速排序中对给定的范围需要选定一个切分元素（“轴”元素 pivot），接下来保证比它大的元素在切分元素后面，比它小的在前面，不断缩小范围，直到完成排序。这就好像给 N 个班混在一起的考试卷分开一样，先大体上分成几小堆，再继续分（先忽略那个 move_pivot_to_first 函数）：

template <typename T>
int part(T* start, int left, int right) {
    move_pivot_to_first(start, left, right);
    int l_cursor = left, r_cursor = right + 1;
    T partition = start[left];
    while (true) {
        while (start[++l_cursor] < partition) if (l_cursor == right) break;
        while (start[--r_cursor] > partition) ;/*if (r_cursor == left) break;*/
        if (l_cursor >= r_cursor) break;
        std::swap(start[l_cursor], start[r_cursor]);
    }
    std::swap(start[left], start[r_cursor]);
    return r_cursor;
}
template <typename T>
void quick_sort(T* start, int left, int right) /* 闭区间 */ {
    if (right <= left) return;
    int partition = part(start, left, right);
    quick_sort(start, left, partition - 1);
    quick_sort(start, partition + 1, right);
}

每次进行切分的步骤是：规定切分元素是某段数组的首个元素，略过数组首个元素，向右移动左指针，直到它不小于切分元素大小或达到右边界，这时左指针以左全是小于切分元素的值；向左移动右指针，直到它不大于切分元素（不用检查是不是到了左边界，左边最前面就是切分元素，最坏情况会停在切分元素上），这时它右边的值全部大于切分元素；检查左右指针相对位置，如果有重叠，说明已经完成切分，此时把首个元素和右指针指向元素进行交换即可（为什么交换右指针指向元素？因为首个元素在左侧，交换后必须保证它小于等于切分元素，而此时左指针已经移出小于切分元素值的区域了，可能指向的是第一个大于切分元素值的元素）；如果不重叠，直接交换左右指针指向的元素，再继续进行这一步骤。
完成切分之后，返回切分元素的位置（右指针），这样就把数组切成两小段，再继续切分。
由此可见，如果选择的切分元素大小处在待排序元素的中位数附近，那么两个子数组长度接近，可以使得递归的深度更小（接近 log N），每层合计需要遍历所有元素，则其时间复杂度为 O(nlog n)。然而，如果每次切分所选择的都是最大或者最小的元素——如这个数组本来就是有序的，那么递归的深度为 N，此时整个排序过程成为 O(N²) 的时间复杂度，这显然是我们不希望的。因此，一味地选取数组首个元素作为切分元素是不合适的，在这里我们采用三取样切分，取首个元素下一位，中间，末尾三个值的中位数与数组首个元素交换以减少最坏情况的发生（这里参考了 gcc 11.1.0 的 std::__move_median_to_first 函数）：

template<typename T>
void move_pivot_to_first(T *array, int left, int right) {
    int middle = (right - left) / 2 + left; // 防 int 溢出
    if (array[left + 1] < array[right]) {
        if (array[right] < array[middle])  {
            std::swap(array[left], array[right]);
            return;
        }
        if (array[middle] < array[left + 1]) {
            std::swap(array[left], array[left + 1]);
            return;
        }
        std::swap(array[left], array[middle]);
        return;
    }
    if (array[left + 1] < array[middle]) {
        std::swap(array[left + 1], array[left]);
        return;
    }
    if (array[middle] < array[right]) {
        std::swap(array[right], array[left]);
        return;
    }
    std::swap(array[middle], array[left]);
}

可以看出，快速排序对于随机性强的数据更有优势，而对于已经部分有序的数据，则不能利用这种有序性。快速排序是原地排序算法，但我们的实现版本需要递归，当每次切分元素都较为均匀时，递归深度接近 log₂N，此时空间复杂度为 O(log N)（由于栈是先入后出的，此时递归二叉树的另一半还没有长出来，另一半生长出来时左边已经释放了，而我们只考虑同一时间占用的最大内存）；当每次切分元素都是两端的元素时，空间复杂度达到了 O(n)。此外，快速排序是不稳定的排序算法，如果左右指针指向的元素大小相同，并且他们被分别切到了左右两边，那么这对元素仍然会被交换位置。

7. 堆排序

堆排序 (Heap Sort) 的一种实现方法是为元素创建最大堆，每次取出堆顶最大元素并移动到数组的最后，从而得到有序数组。在建堆过程中，由上而下进行有序化，保证节点大于其儿子节点的过程成为下沉 (sink)；由下而上进行有序化，保证节点小于其父亲的过程称为上浮 (swim)。在输入数组中构造堆时，可以自顶向下推进，依次把末尾的新节点上浮，也可以自底向上，依次把新节点下沉。自底向上建堆时，可以把后一半的节点（叶子节点）省掉，且插入大量底部节点时树高较小，插入少量顶部节点时树高较大，更加合理，但判断与哪个儿子交换时会略微复杂。我们采用自底向上建堆的方法建立最大堆。之后，我们将堆顶的元素与最后一个元素交换，这时最后一个元素是最大元素，我们把它排除在堆外，即令堆的大小减 1，再从堆顶进行下沉操作，得到新的最大堆，再取堆顶与倒数第二个元素交换，这样一直进行下去：

/* Make sure that the pointer start points at the top of the heap, 
otherwise we can't access the children by 2 * start_position + 1/ + 2 */
template <typename T> void sink(T *start, int start_position,  int scale) {
    while (true) {
        if (2 * start_position + 1 >= scale) break;
        if (2 * start_position + 2 >= scale) { /* only left child */
            if (start[2 * start_position + 1] > start[start_position]) {
                T temp = start[start_position];
                start[start_position] = start[2 * start_position + 1];
                start[2 * start_position + 1] = temp;
            }
            break;
        }
        if (start[2 * start_position + 1] > start[2 * start_position + 2]) { /* left child bigger than right*/          
            if (start[2 * start_position + 1] > start[start_position]) { /* left bigger than father */
                T temp = start[start_position];
                start[start_position] = start[2 * start_position + 1];
                start[2 * start_position + 1] = temp;
                start_position = 2 * start_position + 1;
                continue;
            } else break;
        }
        /* right child bigger than left */
        if (start[2 * start_position + 2] > start[start_position] /* right child bigger than father*/) {
            T temp = start[start_position];
            start[start_position] = start[2 * start_position + 2];
            start[2 * start_position + 2] = temp;
            start_position = 2 * start_position + 2;
            continue;
        } else break;
    }
}
template <typename T>
void heap_sort(T *start, int length) {
    // firstly build heap
    for (int sink_start = length / 2 - 1; sink_start >= 0; --sink_start) {
        sink(start, sink_start, length);
    }
    // secondly swap the top elem with the last and sink the top again
    for (int i = 1; i < length; ++i) {
        T top = *start;
        *start = *(start + length - i);
        *(start + length - i) = top;

        sink(start, 0, length - i);
    }
}

建堆时我们自底向上地建堆，假设这个堆有 N = 2^k-1 个元素，建立自底向上第 i 层时共有 $\frac{N+1}{2^i}$ 个元素，每个元素下沉时最多比较 2(i-1) 次，总比较次数 $\sum_{i-1}^{\log_{2}(N+1)}{\frac{N+1}{2^i}\cdot{}{2(i-1)}}$ ，经错位相减求和可知，建堆需要 O(n) 时间复杂度；每次删除最大元素后的调整是 log n 级别的，全部删除元素需要 O(nlog n) 时间复杂度，故整个堆排序的时间复杂度为 O(nlog n)。但是，堆排序比较大小的数据（儿子节点、父亲节点）在内存中常常不连续，而快速排序访问连续的数据的比重更大，根据局部性原理，快速排序对 cache 等利用效率更高，要更快一些。
堆排序是原地排序，空间复杂度为 O(1)。堆排序也不是稳定的排序算法：9 4 4 -> 4 4 9
R.W. Floyd 提出^[3]，由于建堆后数组末尾的元素均是较小的元素，它们在交换到堆顶后大概率还会下沉到很靠近堆底的部分，在每次取出最大元素后可以先另外暂存占用的数组末尾的那个元素，然后从堆顶开始，把较大的儿子节点覆盖到堆顶，再把大儿子的大儿子节点覆盖大儿子，一直到堆底，这时再把暂存的元素放到停下来的位置，从这里开始做上浮操作，这样能避免传统方法（从堆顶下沉）中不必要的比较大小（不用把堆顶和左右节点比较了），虽然看起来额外增加了一段路程，但总体上是减少了比较次数的：

template <typename T> void swim(T *start, int node_pos) {
    while (node_pos) {
        if (start[(node_pos - 1) / 2] < start[node_pos]) {
            T temp = start[node_pos];
            start[node_pos] = start[(node_pos - 1) / 2];
            node_pos = (node_pos - 1) / 2;
            start[node_pos] = temp;
        } else break;
    }
}
template <typename T> void heap_sort_floyd(T *start, int length) {
    for (int sink_start = length / 2 - 1; sink_start >= 0; --sink_start) {
        sink(start, sink_start, length);
    }
    
    for (int i = 1; i < length; ++i) {
        T end = *(start + length - i);
        *(start + length - i) = *start;
        int new_pos = 0;
        while (true) {
            if (new_pos * 2 + 1 >= length - i) break;
            if (new_pos * 2 + 2 >= length - i) { // only left child
                //if (start[new_pos * 2 + 1] > start[new_pos]) {
                    start[new_pos] = start[new_pos * 2 + 1];
                    new_pos = new_pos * 2 + 1;
                //}
                break;
            }
            if (start[new_pos * 2 + 1] > start[new_pos * 2 + 2]) {
                start[new_pos] = start[new_pos * 2 + 1];
                new_pos = new_pos * 2 + 1;
            } else {
                start[new_pos] = start[new_pos * 2 + 2];
                new_pos = new_pos * 2 + 2;
            }
        }
        start[new_pos] = end;
        swim(start, new_pos);
    }
}

8. 计数排序

计数排序（Counting Sort）可以通过用元素值直接访问数组来统计比某个元素小的元素的个数，从而得出元素排序后的数组下标来实现排序：

template <typename T> void counting_sort(T *start, int elem_num, int array_size) {
    int *times = new int[array_size];
    memset(times, 0, sizeof(int) * array_size);
    int *offset = new int[elem_num];
    for (int i = 0; i < elem_num; ++i) {
        ++times[start[i]];
    }
    for (int i = 1; i < array_size; ++i) {
        times[i] += times[i - 1];
    }
    for (int i = elem_num - 1; i >= 0; --i) {
        offset[i] = --times[start[i]];
    }
    
    for (int i = 0; i < elem_num; ++i) {
        while (offset[i] != i) {
            T temp = start[i];
            start[i] = start[offset[i]];
            start[offset[i]] = temp;
            std::swap(offset[i], offset[offset[i]]);
        }
    }
    delete[] times;
    delete[] offset;
}

此排序算法要求待排序元素的键值必须能作为数组下标，且要求我们知道待排序元素的取值范围。我们申请一个与取值范围相同的数组并赋初值为 0，之后通过元素的键值直接访问该数组，将对应值加 1，直到遍历全部元素。之后，从前到后地，把取值范围数组中（从第二个元素开始）每个位置上的元素与前一个位置上的元素相加并赋值给这个位置，这样这个位置下标的值就是从小到大访问到这个元素时，总共已经有了多少元素。遍历完后，可以新建一个临时数组以保存排序结果，从后往前遍历源数组，把源数组元素值作为下标访问取值范围数组，得到的值就是其在临时数组中的下标，之后再把刚刚用源数组元素值访问范围数组得到的值 - 1 后写回。通过倒序遍历、减一写回，我们实现了排序的稳定性。但是不同版本计数排序实现不同，代码中的版本是不开辅助数组的版本，仍然保证了排序的稳定性。
计数排序正是一种不基于比较的排序算法。以上代码排序 int 时的时间复杂度为 O(n+k)，空间复杂度为 O(k)，其中 k 为数字的范围。当 n+k < nlog n 时，计数排序可以实现对快速排序等基于比较的排序算法的超越。然而如果数据过于稀疏，n+k 甚至会远大于 nlog n。

9. 桶排序

我曾经突发奇想，能不能直接利用自然数作为数组下标来访问数组的方式实现排序呢？于是我写下了类似的代码：

// Due to the lack of memory, we only allow [0, 2147483646] here.
void pigeonhole_sort(int *start, int elem_num, int max_value) {
    int *array = new int[max_value + 1];
    memset(array, -1, sizeof(int) * (max_value + 1));
    for (int i = 0; i < elem_num; ++i) {
        ++array[start[i]];
    }
    int i = 0;
    for (int j = 0; j < max_value + 1; ++j) {
        while (~array[j]) {
            start[i++] = j;
            --array[j];
            if (i == elem_num) {
                j = max_value;
                break;
            }
        } 
    }
    delete[] array;
}

虽然开一个 2147483647 长度的整型数组需要大概 8GB 的内存（而且大多数情况下不会有 2147483647 个重复的元素，也就用不到 int 来存放相同元素的个数），但这种朴素的排序算法（鸽巢排序，Pigeonhole Sort）其实正是桶排序 (Bucket Sort) 的雏形。桶排序先用某些键值将元素装进不同的桶里以缩小问题规模，然后常常通过其他排序方式继续对同一个桶中的元素进行排序，最后将桶中的元素依次拿出按顺序放在一起。比如说要对某些日期排序时，先按月份排好，再在每个月份中按日期进行排序。下面的代码通过将 [0, 1) 之间的数据分成 10 个“桶”，然后对每个桶中的链表进行插入排序实现桶排序：

// [0, 1)
void bucket_sort_0to1(double* src, size_t len) {
    Node** list = new Node*[10];
    memset(list, 0, sizeof(Node*) * 10);
    for (size_t i = 0; i < len; ++i) {
        Node** ptr = &list[(int)(src[i] * 10)];
        while (*ptr) {
            if ((*ptr)->val <= src[i])
                ptr = &(*ptr)->next;
            else
                break;
        }
        *ptr = new Node{src[i], *ptr};
    }
    size_t i = 0, j = 0;
    while (i != len) {
        Node* ptr = list[j++];
        while (ptr) {
            src[i] = ptr->val;
            ptr = ptr->next;
            ++i;
        }
    }
    for (int i = 0; i < 10; ++i) {
        delete list[i];
    }
    delete[] list;
}

在这段代码中，当元素均匀分布在 [0, 1) 中时，将元素分为 k 桶需要 O(n) 时间复杂度，而对每一桶元素使用插入排序时间复杂度为 $O(\frac{n^2}{k^2})$，因此总时间复杂度为 $O(n+\frac{n^2}{k})$。当 k 接近于 n 时（接近鸽巢排序），此时总时间复杂度接近 O(n)。然而，最坏情况下，所有元素集中在同一个桶，此时桶排序退化为插入排序，时间复杂度为 O(n²)。此外，如果桶的个数 k 远多于 n 时，此时桶排序效率也不够理想。
桶排序空间复杂度为 O(n+k)，是稳定的排序算法。

10. 基数排序

当我们比较整数时，常常是由高到低按位比较的，能否依照此思想设计一种排序算法呢？基数排序（Radix Sort）正是一种对各元素从低位到高位先放入个数等于进制数的桶中，再将各桶中的元素按顺序取出，直到整个数组中的元素均有序的排序算法。可以看出，该算法的实现依赖于桶排序的稳定性：

template <typename T> void radix_sort_linkedlist(T *src, int base, int len) {
    struct Node {Node * next; T elem;};
    Node **list = new Node*[base];
    T *sorted = new T[len];
    memset(list, 0, sizeof(Node*) * base);
    for (int i = 0; i < len; ++i) {
        sorted[i] = src[i];
    }
    int i = base, k = 1;
    while (true) {
        for (int j = 0; j < len ; ++j) {
            if (!list[sorted[j] % i / k]) {
                list[sorted[j] % i / k] = new Node{nullptr, sorted[j]};
            } else if (list[sorted[j] % i / k]->elem > sorted[j]) {
                list[sorted[j] % i / k] = new Node{list[sorted[j] % i / k], sorted[j]}
            } else {
                Node *now = list[sorted[j] % i / k];
                while (now->next && now->next->elem < sorted[j]) now = now->next;
                now->next = new Node{now->next, sorted[j]};
            }
        }
        int sorted_elem_num = 0, curr_base = 0;
        while (sorted_elem_num < len) {
            Node *curr_node = list[curr_base++];
            while (curr_node) {
                sorted[sorted_elem_num++] = curr_node->elem;
                curr_node = curr_node->next;
            }
        }
        for (int j = 0; j < base; ++j) {
            Node *curr_del = list[j];
            while (curr_del) {
                Node *temp = curr_del->next;
                delete curr_del;
                curr_del = temp;
            }
        }
        memset(list, 0, sizeof(Node*) * base);
        if (curr_base == 1) break;
        i = i * base;
        k = k * base;
    }
    for (int i = 0; i < len; ++i) {
        src[i] = sorted[i];
    }
    delete[] list;
    delete[] sorted;
}

在这里，我们对每一位进行桶排序时，实际上可以利用计数排序的思想直接计算出每个元素在拼接出新数组的位置，从而摆脱有形的“桶”：

template <typename T> void radix_sort(T *src, int len, long base) {
    T * const initial_src = src;
    T *copy = new T[len];
    long curr_base = base, last_base = 1;
    int *count = new int[base];
    while (true) {
        memset(count, 0, sizeof(int) * base);
        bool has_nonzero_group = false;
        for (int i = 0; i < len; ++i) {
            if (src[i] / last_base) has_nonzero_group = true;
            ++count[src[i] % curr_base / last_base];
        }
        if (!has_nonzero_group) break;
        for (int i = 1; i < base; ++i) {
            count[i] += count[i - 1];
        }
        for (int i = len - 1; i >= 0; --i) {
            copy[--count[src[i] % curr_base / last_base]] = src[i];
        }
        T *temp = src;
        src = copy;
        copy = temp;
        last_base = curr_base;
        curr_base *= base;
    }
    if (initial_src != src) {
        T *temp = copy;
        copy = src;
        src = temp;
        for (int i = 0; i < len; ++i) {
            src[i] = copy[i];
        }
    }
    delete[] copy;
    delete[] count;
}

这里我们每次的模 curr_base 都会与进制数 base 相乘，相当于元素中进行比较的位每次都会左移，实现从低位到高位的比较，同时除以 last_base 舍弃掉末尾已经比较过的位上的数字，同时使得数在 [0, base) 范围内；用 src 和 copy 两个数组来回交换，省去了部分的元素复制操作。
基数排序是稳定的排序算法，由于从桶中“拿出”到 copy 是按顺序的，相同大小元素的相对位置不变。
基数排序时间复杂度看起来是 O(d(n+k)) ，其中 n 是元素数目，k 是桶的个数，d 是元素的位数，但是 d 与 n 并不是完全无关的：重复元素越少，d 与 n 就越相关，当所有元素均不重复时，$d\geq\log_kn$，此时时间复杂度达到 O(nlog n)级别；当所有元素均大小相等时，时间复杂度为 O(n+k)。不过，我们可以利用计算机多位数比较的硬件能力，将多位数合成一次比较，减少比较次数（认为 CPU 每次比较是等时的，那不妨一次多比较几位）。
基数排序空间复杂度为 O(n+k)。（这里采用了类似计数排序的处理方式）
显然上面的代码在元素能转为非负整型值时可以排序，但元素是浮点数呢？查阅互联网后，我了解到，IEEE 754 标准下的浮点数，在不考虑符号位时，具有和整型相似的性质：自低位到高位，各位对结果大小的影响越来越大，且高位有“压倒性”优势，那么我们也可以写出如下的代码：

void radix_sort_double(double *src, const int len, const int base = 256) {
    unsigned long long *src_l = (unsigned long long *)src;
    unsigned long long * const initial_src = src_l;
    unsigned long long *copy = new unsigned long long[len];
    unsigned int *count = new unsigned int[base];
    const unsigned long long FLIP_MSB = (1ull << 63);
    for (int i = 0; i < len; ++i) {
        if (src_l[i] >= FLIP_MSB) src_l[i] = ~src_l[i];
        else src_l[i] ^= FLIP_MSB;
    }
    for (int eightbit = 0; eightbit < 8; ++eightbit) {
        memset(count, 0, sizeof(int) * base);
        unsigned char *bit = reinterpret_cast<unsigned char *>(src_l) + eightbit; // src_l 和 copy 交换，导致只能使用 src_l 不能用 src

        
        for (int i = 0; i < len; ++i) {
            ++count[(unsigned)*(bit + 8 * i)];
        }
        for (int i = 1; i < base; ++i) {
            count[i] += count[i - 1];
        }

        for (int i = len - 1; i >= 0; --i) {
            if (count[(unsigned)*(bit + 8 * i)] == 0) abort();
            copy[--count[(unsigned)*(bit + 8 * i)]] = src_l[i];
        }
        unsigned long long *temp = src_l;
        src_l = copy;
        copy = temp;
    }
    if (initial_src != src_l) {
        unsigned long long *temp = copy;
        copy = src_l;
        src_l = temp;
        for (int i = 0; i < len; ++i) {
            src_l[i] = copy[i];
        }
    }
    for (int i = 0; i < len; ++i) {
        if (src_l[i] >= FLIP_MSB)
        src_l[i] ^= FLIP_MSB;
        else src_l[i] = ~src_l[i];
    }
    delete[] copy;
    delete[] count;
}

这里我们先把负数取反，因为去掉符号位后绝对值大的负数取反后绝对值小，这样稍后排序时就把小的负数排在大的负数前面；同时对整数只对最高位取反，这样负数的符号位（最高为）实际上成了 0，正数的符号位成了 1，这样稍后排序时负数始终在正数前面。之后，我们由低位向高位 一个字节一个字节地排序（x86 采用小端模式，多字节数据，如这里的 double，的低字节在小的地址端，所以指针递增时实际上是由低字节指向高字节，也就是基数排序从低位向高位转移），最后就能得出结果。

Part 2 总结

排序算法多种多样，且一种排序算法常有许多不同的实现，本文只是粗浅地谈到了其中的几种。可以看出，基于比较的排序算法平均时间复杂度不可能低于 nlog n 级别，这是因为一般地，要想将 n 个元素排序完毕，必须确定这 n 个元素之间的相对大小关系。n 个元素相对大小关系共有 n! 种可能（相等被合并进大于或者小于里），而我们每进行一次比较，就把可能的大小关系数减少一半，而 n! 总共需要这样“折半”的次数，是计算 log(n!) = nlog n 级别的。在基于比较的排序算法里，当给出的数据是“随机”的时，快速排序似乎是最快的，但它不是稳定的。如果想要稳定的话，可以考虑归并排序。而当数据总体上是有序时，插入排序则常常是最快的。需要实现优先队列时，可能选择的是堆排序。
实际上，C++ STL (g++ 11.1.0, Linux x86_64) 上 std::sort 使用的是“内省式排序” (Introspective Sort)，在元素个数大于 16 时先进行快速排序（三取样切分），快速排序时发现递归深度超过 2log n 时启动堆排序，最后使用插入排序收尾。而 Java JDK 1.8 排序整型数组时，长度小于等于 47 时采用插入排序，长度大于 47 小于等于 286 ，或是长度大于 286 且相同元素或乱序组过多时根据数据相等的情况，决定是采用双轴快速排序 (Dual Pivot Quicksort) 还是单轴快速排序，长度大于 286 且有序情况好的整型数组采用归并排序^[4]；排序 char、byte 时，数组足够大时将启用计数排序^[5]。此外，Python 还使用了 TimSort，这一排序算法被认为在现实数据（有一定的有序片段）的排序中性能超过快速排序。就算是对于我们已经简单介绍过的这些算法，也仍然有许多值得尝试的思路，如使用迭代而非递归实现快速排序。不幸的是，笔者水平有限，也没有如此的精力。我们必须结尾了。

Part 3 性能测试（娱乐）

下面的代码在 Intel Core i5-10400 的笔记本上编译运行，Linux 内核版本 5.15.2-arch1-1，glibc 版本 2.33-5，g++ 版本 11.1.0：（g++ 开启 O2 优化）：

int main() {
    std::random_device rd;
    std::default_random_engine eng(rd());
    std::uniform_real_distribution<> distr(下界, 上界);
    constexpr size_t LENGTH = 数组长度;
    double test_input_double[LENGTH], test_src[LENGTH], standard_answer[LENGTH];
    for (int i = 0; i < sizeof(test_input_double) / sizeof(double); ++i) {
        standard_answer[i] = test_input_double[i] = distr(eng);
    }
    clock_t start_time = clock();
    sort(standard_answer, standard_answer + sizeof(standard_answer) / sizeof(double));
    cout << "std::sort " <<(double)(clock() - start_time) / CLOCKS_PER_SEC << endl;
    
    memcpy(test_src, test_input_double, sizeof(test_input_double));
    start_time = clock();
    qsort(test_src, LENGTH, sizeof(double), double_cmp);
    cout << "qsort " <<(double)(clock() - start_time) / CLOCKS_PER_SEC << endl;
    for (int i = 0; i < sizeof(test_input_double) / sizeof(double); ++i) {
        if (standard_answer[i] != test_src[i]) {cout<<"qsort dead!"<<endl;abort();}
    }

    memcpy(test_src, test_input_double, sizeof(test_input_double));
    start_time = clock();
    selection_sort(test_src, sizeof(test_input_double) / sizeof(double));
    cout << "Selection Sort " <<(double)(clock() - start_time) / CLOCKS_PER_SEC << endl;
    for (int i = 0; i < sizeof(test_input_double) / sizeof(double); ++i) {
        if (standard_answer[i] != test_src[i]) abort();
    }

    memcpy(test_src, test_input_double, sizeof(test_input_double));
    start_time = clock();
    insertion_sort(test_src, sizeof(test_input_double) / sizeof(double));
    cout << "Insertion Sort " <<(double)(clock() - start_time) / CLOCKS_PER_SEC << endl;
    for (int i = 0; i < sizeof(test_input_double) / sizeof(double); ++i) {
        if (standard_answer[i] != test_src[i]) abort();
    }

    memcpy(test_src, test_input_double, sizeof(test_input_double));
    start_time = clock();
    skipsorted_cocktail_sort(test_src, sizeof(test_input_double) / sizeof(double));
    cout << "Cocktail Sort(Skip Sorted) " <<(double)(clock() - start_time) / CLOCKS_PER_SEC << endl;
    for (int i = 0; i < sizeof(test_input_double) / sizeof(double); ++i) {
        if (standard_answer[i] != test_src[i]) abort();
    }

    memcpy(test_src, test_input_double, sizeof(test_input_double));
    start_time = clock();
    shell_sort(test_src, sizeof(test_input_double) / sizeof(double));
    cout << "Shell Sort " <<(double)(clock() - start_time) / CLOCKS_PER_SEC << endl;
    for (int i = 0; i < sizeof(test_input_double) / sizeof(double); ++i) {
        if (standard_answer[i] != test_src[i]) abort();
    }

    memcpy(test_src, test_input_double, sizeof(test_input_double));
    start_time = clock();
    merge_sort_TopDown(test_src, sizeof(test_input_double) / sizeof(double));
    cout << "Merge Sort(Top Down) " <<(double)(clock() - start_time) / CLOCKS_PER_SEC << endl;
    for (int i = 0; i < sizeof(test_input_double) / sizeof(double); ++i) {
        if (standard_answer[i] != test_src[i]) abort();
    }

    memcpy(test_src, test_input_double, sizeof(test_input_double));
    start_time = clock();
    quick_sort(test_src, 0,  sizeof(test_input_double) / sizeof(double) - 1);
    cout << "Quick Sort " <<(double)(clock() - start_time) / CLOCKS_PER_SEC << endl;
    for (int i = 0; i < sizeof(test_input_double) / sizeof(double); ++i) {
        if (standard_answer[i] != test_src[i]) abort();
    }

    memcpy(test_src, test_input_double, sizeof(test_input_double));
    start_time = clock();
    heap_sort_floyd(test_src, sizeof(test_input_double) / sizeof(double));
    cout << "Heap Sort (Floyd) " <<(double)(clock() - start_time) / CLOCKS_PER_SEC << endl;
    for (int i = 0; i < sizeof(test_input_double) / sizeof(double); ++i) {
        if (standard_answer[i] != test_src[i]) abort();
    }

    memcpy(test_src, test_input_double, sizeof(test_input_double));
    start_time = clock();
    radix_sort_double(test_src, int(sizeof(test_input_double) / sizeof(double)));
    cout << "Radix Sort " <<(double)(clock() - start_time) / CLOCKS_PER_SEC << endl;
    for (int i = 0; i < sizeof(test_input_double) / sizeof(double); ++i) {
        if (standard_answer[i] != test_src[i]) abort();
    }    
}

改变数组的长度，下界，上界，每次运行 3 次取平均时间，对随机序列浮点数排序：
当上下界为 (-1000, 1000) 时：

数组长度	100	1000
std::sort	7.66667E-06	0.000111667
qsort	1.33333E-05	0.000197
选择排序	1.36667E-05	0.001195667
插入排序	1.03333E-05	0.000722333
跳过有序部分的鸡尾酒排序	0.000024	0.001728667
希尔排序	0.000007	9.73333E-05
自顶向下归并排序	1.03333E-05	0.000105667
快速排序	0.000008	9.93333E-05
Floyd 优化堆排序	0.000009	0.000113333
基数排序	1.33333E-05	0.000046

当上下界为 (-1000000, 1000000) 时：

数组长度	100	1000
std::sort	1.30E-05	0.000147333
qsort	2.20E-05	0.000278
选择排序	2.30E-05	0.001250333
插入排序	1.63E-05	0.001108
跳过有序部分的鸡尾酒排序	3.83E-05	0.002401667
希尔排序	1.07E-05	0.000148667
自顶向下归并排序	1.67E-05	0.000158
快速排序	1.37E-05	0.000148
Floyd 优化堆排序	1.37E-05	0.000170333
基数排序	2.33E-05	6.53333E-05

总的来说，数据范围小时，排序似乎更快，以下几组都在 (-1000, 1000) 中测出（这几组由于长度比较长，没有重复实验）：

数组长度	10000	100000	1000000
std::sort	0.000936333	0.012468	0.071469
qsort	0.001347	0.012289333	0.111367
选择排序	0.033825	2.86037	333.48
插入排序	0.033676	3.161943333	341.91
跳过有序部分的鸡尾酒排序	0.091149667	9.482406667	1009.35
希尔排序	0.000645333	0.008864	0.12158
自顶向下归并排序	0.000623333	0.008097667	0.097622
快速排序	0.000550333	0.006777	0.080969
Floyd 优化堆排序	0.000673333	0.009133667	0.128802
基数排序	0.000163	0.002073333	0.028749

仅仅是为了好玩，我又测量了 200000，300000，…，900000 的情况，得到：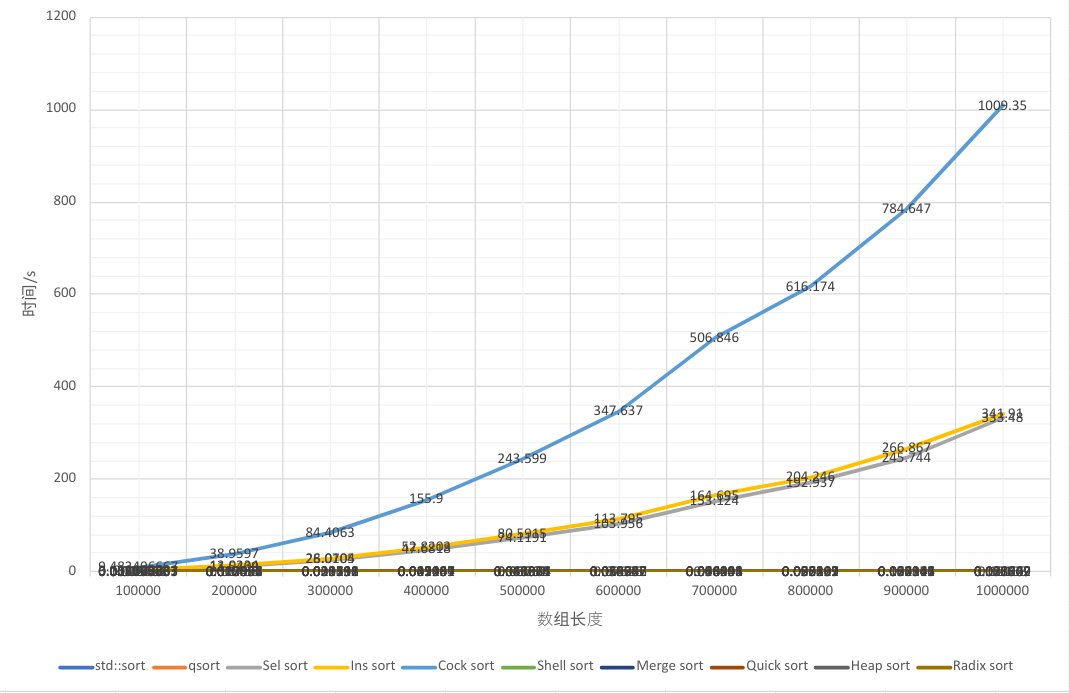


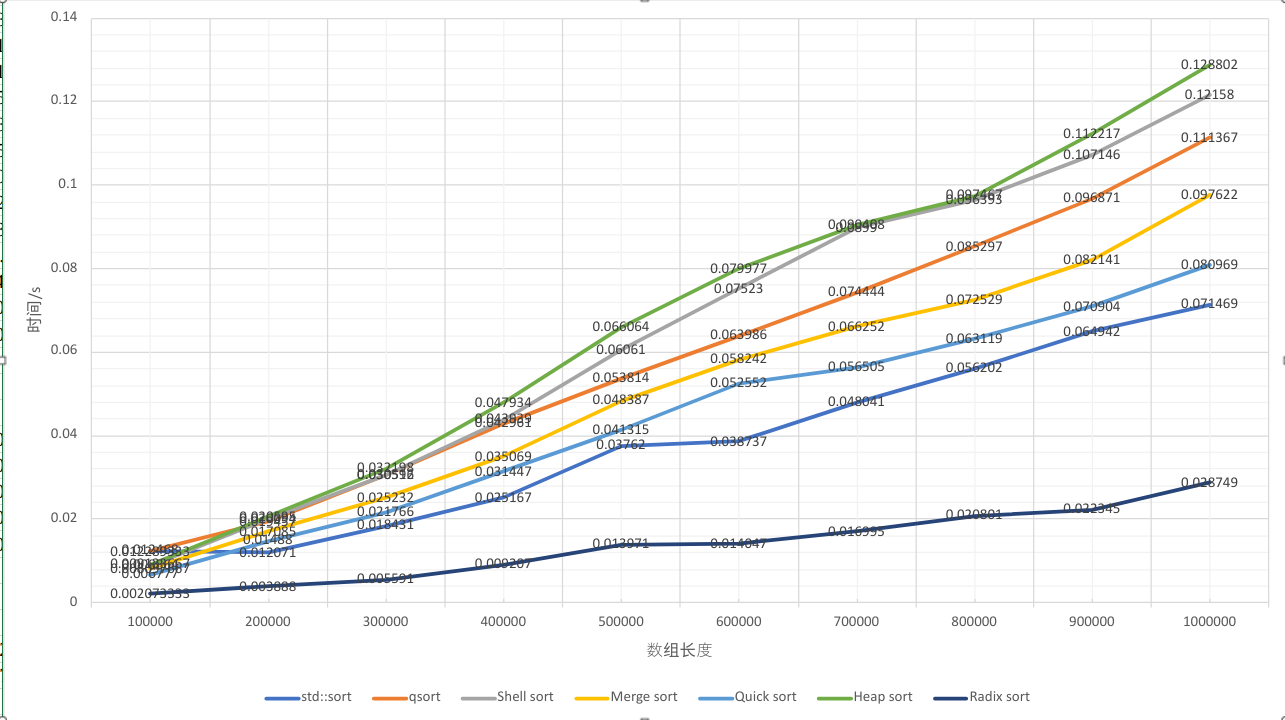
为了考察有序性对性能的影响，当数组长度为 10000，范围 (-1000，1000) 时，测量出完全升序、（第 0，10000，20000，30000，40000，…，90000）随机，其余位置升序、完全降序的情况：

有序性	完全升序	接近升序	完全降序
std::sort	0.001059	0.005846	0.001357
qsort	0.002488	0.002918	0.004248
选择排序	2.84899	3.72152	2.87279
插入排序	8.6e-05	0.000498	6.33238
跳过有序部分的鸡尾酒排序	0.000123	1.48579	6.57123
希尔排序	0.000667	0.00176	0.001462
自顶向下归并排序	0.001812	0.001958	0.002136
快速排序	0.001385	0.115653	0.001515
Floyd 优化堆排序	0.004723	0.004694	0.005258
基数排序	0.002475	0.002295	0.002025

为了了解整型的情况，我又对 (0, 1000000) 的正整数排序进行测试，这次将基数排序替换为整型版本，并加入了计数排序：

数组长度	10000	100000	1000000
std::sort	0.001190667	0.005622667	0.068292
qsort	0.002274667	0.009722333	0.104763
选择排序	0.046129	2.66948	308.974
插入排序	0.031989	2.98289	311.727
跳过有序部分的鸡尾酒排序	0.077564667	8.208996667	857.231
希尔排序	0.000599	0.00847	0.110247
自顶向下归并排序	0.000569667	0.007658667	0.095276
快速排序	0.000516333	0.006403333	0.071781
Floyd 优化堆排序	0.000665667	0.00898	0.131631
基数排序	0.001474	0.014975667	0.134972
计数排序	0.0004	0.002697667	0.062725

由于 O2 优化等因素的影响，实际得到的结果与预想有些出入。
总之，尽管排序算法性能差距悬殊，可有时人和人之间的差别比这还大呢！

1. 《算法（第 4 版）》P154 ↩
2. http://blog.sciencenet.cn/blog-83029-468247.html ↩
3. 《算法（第 4 版）》P208 ↩
4. https://cloud.tencent.com/developer/article/1690708?from=article.detail.1394343 ↩
5. https://blog.csdn.net/qq_45557225/article/details/105956950 ↩