进制转换

（无数的人已经写过这篇了）

首先介绍一下相关英文：

进制 Base

二进制 Binary

八进制 Octal

十进制 Decimal

十六进制 Hexadecimal

接下来探讨一下其转换。

Part 1 整数部分

进制虽然不同，但其表示思想类似，即每一数位上的数字均代表进位的 n 次幂的倍数。因此，我们把其余数制转为十进制是直观容易的：

FEC (base 16) → 15×16²+14×16+12 (base 10)

如何将十进制转为其他进制呢？只需逆向以上过程：

1492 (base 10) → 512×2+64×7+8×2+1×4 (base 10) →2724 (base 8)

这样，以十进制为桥梁，可以实现进制转换。

针对十进制转二进制，可以使用长除法，应用“先余为低，后余为高”：（最先得出的余数可以认为代表低数位）

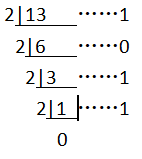
将 13 转为二进制，结果为 1101。

此外，由于除了十进制外的十六进制、八进制的进制数都是 2 的幂，我们也可以从二进制直接转至十六进制或八进制。举个例子，对于 111110110 (base 2) = 766 (base 8)，由于 2³=8 ，从右向左三位三位地分节，将每一节所对应的三位二进制数转为一位八进制后按原节次序排列即可。十六进制同理。

同样地，也可以用此方法将十六进制、八进制转为二进制，记得补 0 以占位。

Part 2 小数部分

一个数的小数部分实质上是当 n 的指数为负数时对整数部分的扩展，对于其他进制转为十进制，这不难理解。但十进制往外转时，除以 n 的负数次幂再取余这一过程可以转成不断对小数部分乘以进制数且按照“先整为高，后整为低”原则取出商数：对于 0.375 (base 10) 转成二进制：

0.375×2=0.75 -> 0

0.75×2=1.5 -> 1

0.5×2=1 -> 1

化为 0.011 (base 2)。